У матэматыцы бэта-функцыяй (Β-функцыяй, бэта-функцыяй Эйлера або Эйлеравым інтэгралам I-га роду ) называецца наступная спецыяльная функцыя ад двух зменных:
Бэта-функцыя Названа ад
Леанард Эйлер Формула, якая апісвае закон або тэарэму
B
(
z
,
w
)
=
∫
0
1
t
z
−
1
(
1
−
t
)
w
−
1
d
t
{\displaystyle \operatorname {B} (z,w)=\int \limits _{0}^{1}t^{z-1}(1-t)^{w-1}\mathrm {d} t}
[1]
B
(
z
,
w
)
=
Γ
(
z
)
Γ
(
w
)
Γ
(
z
+
w
)
{\displaystyle \operatorname {B} (z,w)={\frac {\operatorname {\Gamma } (z)\operatorname {\Gamma } (w)}{\operatorname {\Gamma } (z+w)}}}
[1] Пазначэнне ў формуле
B
(
z
,
w
)
{\displaystyle \operatorname {B} (z,w)}
∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x}
Γ
(
z
)
{\displaystyle \operatorname {\Gamma } (z)}
Медыяфайлы на Вікісховішчы
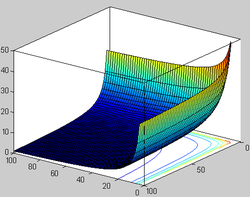
Графік бэта-функцыі пры рэчаісных аргументах
B
(
x
,
y
)
=
∫
0
1
t
x
−
1
(
1
−
t
)
y
−
1
d
t
,
{\displaystyle \mathrm {B} (x,y)=\int \limits _{0}^{1}t^{x-1}(1-t)^{y-1}\,dt,}
вызначаная пры
ℜ
(
x
)
>
0
,
{\displaystyle \Re (x)>0,}
ℜ
(
y
)
>
0.
{\displaystyle \Re (y)>0.}
Бэта-функцыя была даследавана Эйлерам і Лежандрам , А назву ёй даў Жак Бінэ .
Бэта-функцыя сіметрычная адносна перастаноўкі зменных, гэта значыць
B
(
x
,
y
)
=
B
(
y
,
x
)
.
{\displaystyle \mathrm {B} (x,y)=\mathrm {B} (y,x).}
Бэта-функцыю можна выразіць праз іншыя функцыі:
B
(
x
,
y
)
=
Γ
(
x
)
Γ
(
y
)
Γ
(
x
+
y
)
,
{\displaystyle \mathrm {B} (x,y)={\frac {\Gamma (x)\Gamma (y)}{\Gamma (x+y)}},}
дзе
Γ
(
x
)
{\displaystyle \Gamma (x)}
гама-функцыя ;
B
(
x
,
y
)
=
2
∫
0
π
/
2
sin
2
x
−
1
θ
cos
2
y
−
1
θ
d
θ
,
ℜ
(
x
)
>
0
,
ℜ
(
y
)
>
0
;
{\displaystyle \mathrm {B} (x,y)=2\int \limits _{0}^{\pi /2}\sin ^{2x-1}\theta \cos ^{2y-1}\theta \,d\theta ,\qquad \Re (x)>0,\ \Re (y)>0;}
B
(
x
,
y
)
=
∫
0
∞
t
x
−
1
(
1
+
t
)
x
+
y
d
t
,
ℜ
(
x
)
>
0
,
ℜ
(
y
)
>
0
;
{\displaystyle \mathrm {B} (x,y)=\int \limits _{0}^{\infty }{\frac {t^{x-1}}{(1+t)^{x+y}}}\,dt,\qquad \Re (x)>0,\ \Re (y)>0;}
B
(
x
,
y
)
=
1
y
∑
n
=
0
∞
(
−
1
)
n
(
y
)
n
+
1
n
!
(
x
+
n
)
,
{\displaystyle \mathrm {B} (x,y)={\frac {1}{y}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(y)_{n+1}}{n!(x+n)}},}
дзе
(
x
)
n
{\displaystyle (x)_{n}}
фактарыял , роўны
x
⋅
(
x
−
1
)
⋅
(
x
−
2
)
⋅
…
⋅
(
x
−
n
+
1
)
.
{\displaystyle x\cdot (x-1)\cdot (x-2)\cdot \ldots \cdot (x-n+1).}
Як гама-функцыя для цэлых лікаў з’яўляецца абагульненнем фактарыяла, так і бэта-функцыя з’яўляецца абагульненнем бінаміяльных каэфіцыентаў з трохі змененымі параметрамі:
C
n
k
=
1
(
n
+
1
)
B
(
n
−
k
+
1
,
k
+
1
)
.
{\displaystyle \mathrm {C} _{n}^{k}={\frac {1}{(n+1)\mathrm {B} (n-k+1,k+1)}}.}
Частковыя вытворныя у бэта-функцыі наступныя:
∂
∂
x
B
(
x
,
y
)
=
B
(
x
,
y
)
(
Γ
′
(
x
)
Γ
(
x
)
−
Γ
′
(
x
+
y
)
Γ
(
x
+
y
)
)
=
B
(
x
,
y
)
(
ψ
(
x
)
−
ψ
(
x
+
y
)
)
,
{\displaystyle {\partial \over \partial x}\mathrm {B} (x,y)=\mathrm {B} (x,y)\left({\Gamma ^{\prime }(x) \over \Gamma (x)}-{\Gamma ^{\prime }(x+y) \over \Gamma (x+y)}\right)=\mathrm {B} (x,\;y)(\psi (x)-\psi (x+y)),}
дзе
ψ
(
x
)
{\displaystyle \psi (x)}
дыгама-функцыя .
Няпоўная бэта-функцыя
правіць
Няпоўная бэта-функцыя — гэта абагульненне бэта-функцыі, якое замяняе інтэграл па адрэзку
[
0
,
1
]
{\displaystyle [0,1]}
B
x
(
a
,
b
)
=
∫
0
x
t
a
−
1
(
1
−
t
)
b
−
1
d
t
.
{\displaystyle \mathrm {B} _{x}(a,b)=\int \limits _{0}^{x}t^{a-1}\,(1-t)^{b-1}\,dt.}
Пры
x
=
1
{\displaystyle x=1}
Рэгулярызаваная няпоўная бэта-функцыя
правіць
Рэгулярызаваная няпоўная бэта-функцыя вызначаецца праз поўную і няпоўную бэта-функцыі:
I
x
(
a
,
b
)
=
B
x
(
a
,
b
)
B
(
a
,
b
)
.
{\displaystyle I_{x}(a,b)={\frac {\mathrm {B} _{x}(a,b)}{\mathrm {B} (a,b)}}.}
Уласцівасці рэгулярызаванай няпоўнай бэта-функцыі:
I
0
(
a
,
b
)
=
0
;
{\displaystyle I_{0}(a,b)=0;}
I
1
(
a
,
b
)
=
1
;
{\displaystyle I_{1}(a,b)=1;}
I
x
(
a
,
b
)
=
1
−
I
1
−
x
(
b
,
a
)
;
{\displaystyle I_{x}(a,b)=1-I_{1-x}(b,a);}
I
x
(
a
+
1
,
b
)
=
I
x
(
a
,
b
)
−
x
a
(
1
−
x
)
b
a
B
(
a
,
b
)
.
{\displaystyle I_{x}(a+1,b)=I_{x}(a,b)-{\frac {x^{a}(1-x)^{b}}{aB(a,b)}}.}
Зноскі
Битюцков В. И. Бета-функция // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М .: Советская энциклопедия. — Т. 1. 
Медыяфайлы на Вікісховішчы
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
