Каэфіцыент асіметрыі

Каэфіцые́нт асіме́трыі — велічыня, якая характарызуе асіметрыю размеркавання выпадковай велічыні адносна яе матэматычнага спадзявання. Каэфіцыент асіметрыі можа прымаць дадатныя або адмоўныя значэнні, ці нават быць нявызначаным.

Параўнанне графікаў шчыльнасці размеркаванняў з адмоўнай і дадатнай асіметрыяй.

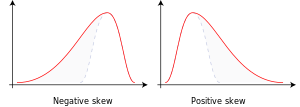
Якасная інтэрпрэтацыя каэфіцыенту асіметрыі складаная. Для размеркавання з адной модай, адмоўны каэфіцыент асіметрыі паказвае, што левы «хвост» функцыі шчыльнасці імавернасці большы або таўсцейшы за правы. З іншага боку, дадатная асіметрыя паказвае, што правы хвост большы. У тых выпадках, калі адзін хвост доўгі, а іншы хвост тоўсты, асіметрыя не падпарадкоўваецца простаму правілу. Напрыклад, нулявое значэнне паказвае, што хвасты па абодва бакі ад матэматычнага спадзявання збалансаваныя. Нулявая асіметрыя мае месца для сіметрычнага размеркавання, але бывае таксама і ў асіметрычных размеркаванняў, дзе асіметрыі ўраўнаважваюць адна другую, напрыклад, адзін хвост доўгі, але тонкі, а іншы — кароткі, але тоўсты. У размеркаваннях з некалькімі модамі і дыскрэтных размеркаваннях каэфіцыент асіметрыі таксама цяжка інтэрпрэтаваць. Важна адзначыць, што асіметрыя не вызначае адносіны сярэдняга і медыяны.

Азначэнне

Асіметрыяй выпадковай велічыні завецца лік

$A={\frac {\mu _{3}}{\mu _{2}^{\frac {3}{2}}}}={\frac {\mu _{3}}{\sigma ^{3}}},$

дзе $\mu _{2}$, $\mu _{3}$ — другі і трэці цэнтральныя моманты, а $\sigma$ — сярэдняе квадратовае адхіленне.

Літаратура

• Звяровіч Э. І., Радына А. Я. Элементы тэорыі імавернасцей. — Мінск: Беларусь, 2013. — ISBN 978-985-01-1043-5.