Спіраль
У матэматыцы, спіраль — гэта крывая, якая агінае некаторы цэнтральны пункт ці вось, паступова набліжаючыся ці аддаляючыся ад яе, у залежнасці ад кірунку абыходу крывой.



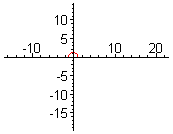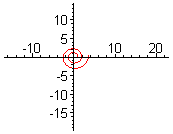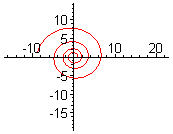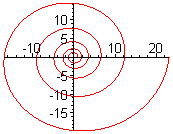
Двухмерныя спіралі
правіцьДвухмерную спіраль можна апісаць у палярных каардынатах, вызначыўшы радыус r як бесперапынную манатонную функцыю ад вугла θ. Акружнасць можна лічыць выраджаным асобным выпадкам спіралі (функцыя не строга манатонная, а з'яўляецца канстантай).
Некаторыя з найбольш важных тыпаў двухмерных спіраляў:
- Архімедава спіраль:
- ;
- Спіраль Ферма:
- ;
- Гіпербалічная спіраль:
- ;
- Лагарыфмічная спіраль:
- ;
- Спіраль Фібаначы (англ.: Fibonacci spiral) і залатая спіраль — асобныя выпадкі лагарыфмічнай спіралі.
Трохмерныя спіралі
правіцьЯк і ў двухмерным выпадку, r — бесперапынную манатонную функцыю ад θ.
Для простых трохмерных спіраляў трэцяя пераменная h — таксама бесперапынная манатонная функцыя ад θ. Напрыклад, канічная вітая лінія можа быць вызначана як спіраль на канічнай паверхні з адлегласцю ад вяршыні як экспанентнай функцыяй ад θ.
Для складаных трохмерных спіраляў, як, напрыклад, сферычная спіраль, h узрастае з ростам θ з аднаго боку ад пункта і змяншацца — з іншай.
Сферычная спіраль
правіцьСферычная спіраль (лаксадрома) — гэта крывая на сферы, якая перасякае ўсё мерыдыяны пад адным вуглом (не прамым). Гэта крывая мае бясконцы лік віткоў. Адлегласць паміж імі змяншацца па меры набліжэння да палюсоў.
Целы, якія маюць форму спіралі
правіць- Ракавіна ў бруханогіх
- Цытакасцяк эўкарыёт
- Спіраль у балансе механічных гадзінікаў
- Спіральная завадная спружына ў механічных гадзінах і ў завадных цацках, спіральная спружына ў стрэлкавых індыкатарах магнітафонаў, радыёпрыёмнікаў, у вымяральных галоўках магнітаэлектрычных галовак амперметраў, вальтметраў, омметраў, тэстараўі інш.
- Цыклон, Антыцыклон
- Спіральныя галактыкі
- Калаген - Фібрылярны бялок з правазакручанай спіраллю
- Рулон
Гл. таксама
правіць| Спіраль на Вікісховішчы |
Літаратура
правіць- Спіра́лі // Беларуская энцыклапедыя: У 18 т. Т. 15: Следавікі — Трыо / Рэдкал.: Г. П. Пашкоў і інш. — Мн. : БелЭн, 2002. — Т. 15. — С. 114. — 10 000 экз. — ISBN 985-11-0035-8. — ISBN 985-11-0251-2 (т. 15).
- Спира́ль // Большая политехническая энциклопедия (руск.) / Авт.-сост. В. Д. Рязанцев. — М.: Мир и образование, 2011. — С. 491—492. — 704 с. — 2 000 экз. — ISBN 978-5-94666-621-3.
- Спира́ли // Т. 24А. Собаки — Струна. — М. : Советская энциклопедия, 1976. — С. 324. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров; 1969—1978). (руск.)