Аналітычная геаметрыя
Аналіты́чная геаме́трыя — раздзел геаметрыі, у якім уласцівасці геаметрычных аб’ектаў (пунктаў, ліній, паверхняў) даследуюцца сродкамі алгебры з дапамогай метаду каардынат. Такі метад вывучэння магчымы пры ўвядзенні сістэмы каардынат, пасля чаго задача зводзіцца да вывучэння ўласцівасцей ураўненняў, якімі задаюцца гэтыя аб’екты.
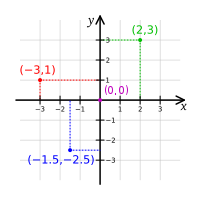
Сістэма каардынат ставіць у адпаведнасць кожнаму пункту прасторы яго каардынаты — набор лікаў. Геаметрычная фігура — гэта мноства пунктаў, кожны з якіх мае свае каардынаты. Калі мноства каардынат усіх пунктаў геаметрычнай фігуры з’яўляецца мноствам рашэнняў пэўнага алгебраічнага выразу, то гэты выраз з’яўляецца аналітычным прадстаўленнем фігуры. Аналітычным прадстаўленнем фігуры можа быць:
Гісторыя правіць
Узнікненне метаду каардынат звязана з развіццём у 17 ст. астраноміі, механікі, тэхнікі. Асновы аналітычнай геаметрыі заклалі Р.Дэкарт (1637) і П.Ферма (1629). Далейшае развіццё звязана з працамі Г.Лейбніца, І.Ньютана, Л.Эйлера, Лагранжа, Г.Монжа, С.Лакруа і інш.
На Беларусі значны ўклад у развіццё аналітычнай геаметрыі зрабілі У. К. Дыдырка («Цыркулярныя крывыя 3-га парадку» — 1-я на Беларусі матэматычная манаграфія, 1928) і І. К. Богаяўленскі («Аналітычная геаметрыя» — 1-ы беларускамоўны падручнік па вышэйшай матэматыцы, 1932).
Асноўны змест правіць
Агульны метад даследавання і класіфікацый ліній і паверхняў прадугледжвае адшуканне такой прамавугольнай сістэмы каардынат, у якой адпаведнае ўраўненне набывае найбольш просты выгляд.
На плоскасці правіць
Асноўная задача аналітычнай геаметрыі на плоскасці — даследаванне ліній 1-га (прамыя) і 2-га (эліпс, гіпербала, парабала) парадку, якія ў дэкартавых каардынатах вызначаюцца алгебраічнымі ўраўненнямі адпаведна 1-й і 2-й ступені.
Плоскасць з’яўляецца двухмернай прасторай, таму аналітычная геаметрыя на плоскасці разглядае алгебраічныя выразы, у якіх фігуруюць дзве пераменныя (x і y), якія адпавядаюць дзвюм каардынатам (абсцысе і ардынаце) яе пунктаў.
Ураўненне віду F(x, y) = 0 задае крывую на плоскасці.
Няроўнасць віду F(x, y) > 0 задае частку плоскасці, абмежаваную крывой.
У трохмернай прасторы правіць
Аналітычная геаметрыя ў прасторы даследуе паверхні 1-га (плоскасці) і 2-га (эліпсоід, гіпербалоід, парабалоід, конус, цыліндр) парадку, якія ў дэкартавых каардынатах вызначаюцца алгебраічнымі ўраўненнямі адпаведна 1-й і 2-й ступені.
Пункт у прасторы вызначаецца трыма каардынатамі, таму аналітычная геаметрыя ў прасторы аперуе алгебраічнымі выразамі з трыма пераменнымі (x, y і z).
Прыкладанні правіць
Метадамі аналітычнай геаметрыі карыстаюцца ў многіх іншых раздзелах матэматыкі, у фізіцы, механіцы, тэхніцы і інш.
Літаратура правіць
- Аналітычная геаметрыя // Беларуская энцыклапедыя: У 18 т. Т. 1: А — Аршын / Рэдкал.: Г. П. Пашкоў і інш. — Мн. : БелЭн, 1996. — Т. 1. — С. 334. — 10 000 экз. — ISBN 985-11-0035-8. — ISBN 985-11-0036-6 (т. 1).
- Тышкевич Р. И., Феденко А. С. Линейная алгебра и аналитическая геометрия. 2 изд. Мн., 1976.